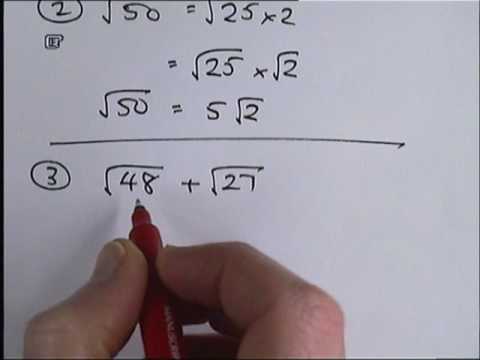Which Form 5495 Index 2017-2025

In this video, we're going to look at simplifying surds. But before we start simplifying them, let's just remind ourselves what they are. Surds are basically nasty square roots. For example, if you have the square root of 10, I'll call that a nasty square root because the decimal is not a whole number. It's a nasty decimal. Therefore, that is a surd. On the other hand, if I did the square root of 16, the square root of 16 is 4 because 4 times 4 is 16. So that's not a surd because the root of 16 is just 4 and 4 is an integer, a whole number. So this one is a surd, whereas this one here is not. The basic thing is that surds are square roots which come out to be nasty decimals. Now, we're going to look at simplifying some surds. The first one we're going to look at is simplifying the square root of 40. The goal of simplifying a surd is to get the smallest number possible inside the square root sign and the other numbers outside the square root sign. To do this, we need to spot what two numbers multiply together to give us 40. So we have one times forty, two times twenty-five, eight times five, and four times ten. We're looking for a pair of numbers where one of them is a square number. In this case, four times ten, four is a square number. So the square root of 40 is the square root of four times ten. And we can simplify this by saying it's the square root of four times the square root of ten. Next, let's consider the square root of 50. We need to think about what numbers multiply together to give us 50. One option...